Eigenvector selection indices for improving milk yield and persistency in Egyptian buffalo
DOI:
https://doi.org/10.56825/bufbu.2022.4134205Keywords:
Bubalus bubalis, buffaloes, eigenvalue, eigenvector selection indices, milk yield, persistency, Egyptian buffaloAbstract
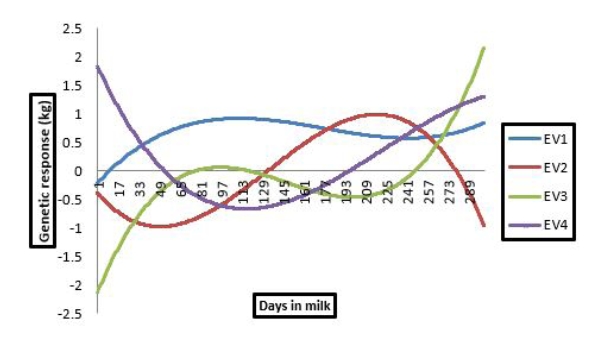
The genetic gains were estimated for milk production and persistency, derived from random regression models, using eigenvector indices, and they were compared with the traditional selection index. The data set contained 4971 test day milk yield recorded for 691 buffalo cows, daughters of 120 sires and 532 dams. The model included the random effects of direct additive genetic, permanent environment and error, whereas the fixed effects were herd test day, year and season of calving and parity, and as a covariate, it was milk days. The first and the 2nd eigenvalues explained 73.1 and 22.9% of the variation of the random regression coefficients, respectively, suggesting that the use of the first two eigenvectors is sufficient. Genetic responses in total milk yield (TMY) based on the first eigenvector index (Ie1) and that based on the conventional selection (IMY) have close gain of about 171 kg in each index. The second eigenvector index (Ie2) showed an increase in TMY (9.91 kg), and thus an increase in the persistency (0.86 kg). The TMY and persistency are the two economically important traits in dairy production, additional genetic gains in persistency and high genetic gain for TMY could be obtained using the 2nd eigenvector index (I*2).
Downloads
Metrics
References
Dekkers, J.C.M., J. Jamrozik, J.H. ten Hag, L.R. Schaeffer and A. Weersink. 1996. Genetic and economic evaluation of persistency in dairy cattle. Interbull Bulletin, 12: 97-102.
Dekkersa, J.C.M., J.H. Ten Hag and A. Weersink. 1997. Economic aspects of persistency in dairy cattle. Livest. Prod. Sci., 53(3): 237-252. DOI: 10.1016/S0301-6226(97)00124-3
Druet, T., F. Jaffrezic, D. Boichard and V. Ducrocq. 2003. Modeling lactation curves and estimation of genetic parameters for first lactation test-day records of French Holstein cows. J. Dairy Sci., 86(7): 2480-2490. DOI: 10.3168/jds.S0022-0302(03)73842-9
EL-Saied, U.M., J.A. Carriedo, L.F. de la Fuente and F.S. Primitivo. 1999. Genetic parameters of lactation cell counts and milk protein yields in dairy ewes. J. Dairy Sci., 82(3): 639-644. DOI: 10.3168/jds.S0022-0302(99)75278-1
Flores, E.B. and J.H.J. van der Werf. 2014. Using random regression models to optimize selection for yield, persistency and calving interval in Philippine dairy buffaloes. In Proceedings of 10th World Congress of Genetics Applied to Livestock Production, Vancouver, Canada.
Geetha, E., A.K. Chakravart and K.V. Kumar. 2006. Genetic persistency of first lactation milk yield estimated using random regression model for Indian Murrah buffaloes. Asian Austral. J. Anim. Sci., 19(12): 1696-1701. DOI: 10.5713/ajas.2006.1696
Hazel, L.N. 1943. The genetic basis for constructing selection indexes. Genetics, 28(6): 476-490. DOI: 10.1093/genetics/28.6.476
Kirkpatrick, M. and N. Heckman. 1989. A quantitative genetic model for growth, shape, reaction norms, and other infinite-dimensional characters. Journal of Mathematic Biology, 27(4): 429-450. DOI: 10.1007/BF00290638
Kirkpatrick, M., D. Lofsvold and M. Bulmer. 1990. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics, 124(4): 979-993. DOI: 10.1093/genetics/124.4.979
Mrode, M.A. 2005. Linear Models for the Prediction of Animal Breeding Values, 2nd ed. CABI Publishing, Wallingford, UK.
Olori, V.E., W.G. Hill, B.J. McGuirk and S. Brotherstone. 1999. Estimating variance components for test day milk records by restricted maximum likelihood with a random regression animal model. Livest. Prod. Sci., 61(1): 53-63. DOI: 10.1016/S0301-6226(99)00052-4
Savegnago, R.P., G.J.M. Rosa, B.D. Valente, L.G.G. Herrera, R.L.R. Carneiro, R.C. Sesana, L. El Faro and D.P. Munari. 2013. Estimates of genetic parameters and eigenvector indices for milk production of Holstein cows. J. Dairy Sci., 96(11): 7284-7293. DOI: 10.3168/jds.2013-6708
Searle, S.R. 1966. Matrix Algebra for the Biological Sciences (Including Applications in Statistics). John Wiley and Sons, Inc., New York, USA. 296p.
Swalve, H.H. 1995. Genetic relationship between dairy lactation persistency and yield. J. Anim. Breed. Genet., 112(1-6): 303-311. DOI: 10.1111/j.1439-0388.1995.tb00570.x
Swalve, H.H. 1998. Use of test day records for genetic evaluation. In Procceding 6th World Congress Genetics Applied to Livestock Production, New South Wales, Australia. 23: 295-302.
Swalve, H.H. 2000. Theoretical basis and computational methods for different test-day genetic evaluation methods. J. Dairy Sci., 83(5): 1115-1124. DOI: 10.3168/jds.S0022-0302(00)74977-0
Togashi, K. and C.Y. Lin. 2004. Efficiency of different selection criteria for persistency and lactation milk yield. J. Dairy Sci., 87(5): 1528-1535. DOI: 10.3168/jds.S0022-0302(04)73304-4
Togashi, K. and C.Y. Lin. 2006. Selection for milk production and persistency using eigenvectors of the random regression coefficient matrix. J. Dairy Sci., 89(12): 4866-4873. DOI: 10.3168/jds.S0022-0302(06)72535-8








.png)








